Top 10 Bodmas Questions

Understanding BODMAS: A Step-by-Step Guide

Source: topperlearning.com

Ever feel lost in a math problem, not sure where to start? BODMAS can help. It's like a special map, telling you the right path through tricky math.

What is BODMAS?

BODMAS is a way to remember the order of steps in math problems.

• Brackets (parentheses) – First
• Orders (powers and roots) – Second
• Division and Multiplication – Third, whichever comes first from left to right.
• Addition and Subtraction – Last, whichever comes first from left to right.

Easy, right?

Why is BODMAS Important?

Math needs rules! Imagine a game with no rules, chaos would follow.

The rule of BODMAS gives a standard way of working out problems. This stops us from getting wrong answers. With the same math, it shows different people get the right answer. Everyone following the same rule helps with a clear result!

How to Apply BODMAS to Simple Expressions

See a problem? Follow the BODMAS rules.

Let's say: 5 + (2 x 3) – 4.

1. Brackets first: (2 x 3) = 6. So we now have 5 + 6 – 4.
2. No more brackets. Division or multiplication come next, no in this problem. So now we have 5 + 6 – 4.
3. Addition/Subtraction (from left to right): 5 + 6 = 11. So now we have 11 – 4.
4. 11 – 4 = 7. That's the answer.

BODMAS with Powers and Roots

Roots and powers are like special multiplication. For example:

2³ x 5 – 10 ÷ 2

1. Powers first: 2³ = 8.
2. Next: Multiplication/Division, left-to-right : 8 x 5 = 40 10 ÷ 2 = 5
3. Now: 40 – 5 = 35. Answer: 35

BODMAS with Brackets and Parentheses

Sometimes brackets show up inside of other brackets!

Example: ** (10 + 5)² – 5 x 2**

1. Work inside the first set of brackets, first: 10+5 = 15 . The problem now looks like (15)² – 5 x 2
2. Next step: 15² (powers). 15 times 15 = 225.
3. Next is multiplication. 5 x 2 = 10 Now we have 225 – 10.
4. Finish the addition/subtraction (in order): 225 – 10 = 215. Your answer!

Common BODMAS Mistakes

Be careful of tricky spots! The common mistake is to miss the left to right part.

People often miss the left-to-right step in multiplication or division. The rules apply, whichever of those two is encountered in order from left to right

Following BODMAS is a useful tool, one that'll take you through hard problems. Now go out there and solve some maths using this rule!

Top 10 Tricky BODMAS Questions to Test Your Skills

Ready to put your BODMAS knowledge to the test? These tricky questions will check how well you understand the order of operations.

Question 1: Simple Arithmetic with BODMAS

Let's start with a simple one: 5 + (2 x 3) – 4

• First, calculate inside the brackets: 2 x 3 = 6. The problem changes to 5 + 6 – 4.
• Next step is addition or subtraction (left to right) : 5 + 6 = 11. So we have 11 – 4 = 7

Question 2: BODMAS with Exponents

Here's a question with a power: 2³ x 5 – 10 ÷ 2.

• First step: find 2 to the power 3 (or 2 raised to the power 3). 2³ = 8. Our problem now is 8 x 5 – 10 ÷ 2.
• Next step is multiplication or division. We solve these operations from left to right order. 8 x 5 = 40. 10 ÷ 2 = 5. Our problem is now 40 – 5.
• Finally: 40 – 5 = 35

Question 3: Evaluating Expressions with Brackets and Multiplication

A problem with brackets and multiplication. Example 10 + 2 * (7-5)

• First step, calculate inside the bracket: 7-5 = 2. This makes it: 10 + 2 * 2
• Now do the multiplication 2 * 2= 4. We have 10 + 4
• Finish with addition. 10+ 4 = 14.

Question 4: BODMAS with Nested Brackets

A step harder: 5 – 2 * (6 + 4 – 8)/ 2.

• Focus on inner brackets, first, following BODMAS (in this case). 6 + 4 = 10 , 10 – 8 = 2 . The new problem: 5 – 2* 2/ 2.
• Next step involves doing multiplication/division first: 2 * 2 = 4 and 4 /2 = 2. New problem : 5 – 2
• Addition/ subtraction : 5 -2=3

Question 5: Complex BODMAS Problem with Multiple Operations

12 – 3 x 4 + 5(6 – 2)

• Tackle the brackets first: 6 – 2 = 4. The new problem is now 12 – 3 * 4 + 5 * 4
• Then, handle multiplication: 3 * 4= 12 , 5 * 4= 20. We now have 12 – 12 +20.
• Lastly, work through addition and subtraction (in order) 12 – 12 + 20 = 20

Question 6: Combining BODMAS with Negative Numbers

Source: cloudfront.net

This question has negatives too: 2(3 + 5) – 1(4 – 6).

• Solve bracket : 3 + 5 = 8 and 4 – 6 =-2. Problem now 2(8) – 1(-2)
• Do multiplication first (following BODMAS). 28= 16 , 1-2 = -2. New problem: 16 – (-2)
• And finish it, solving addition/subtraction: 16 – (-2) = 18

Question 7: Nested Brackets and Division

** (6 ÷ 2)(3 + 2) + 4**

• Solving inner bracket: 3+2=5. Our new problem : (6 ÷ 2)(5) + 4.
• Multiplication/division : 6÷2= 3. Then multiply 3*5 = 15. Now problem is 15 + 4.
• Addition : 15 + 4= 19

These were some tricky questions; remember the order to tackle them successfully. Mastering BODMAS will lead to the accurate solutions every single time, no matter how tricky the equation might look!

7 Common Mistakes to Avoid When Using BODMAS

Source: co.uk

Following BODMAS is important, but making mistakes is normal. Let's learn common errors to avoid them.

1. Incorrect Order of Operations

The most common problem. People forget the correct steps!

• Sometimes, people do addition before multiplication or brackets. The right order matters!
• The rules dictate steps in a specific order: brackets, powers, multiplication/division, then addition/subtraction

2. Misinterpreting Brackets

Brackets (parentheses) are vital, showing what to solve first.

• Sometimes, the wrong bracket part gets overlooked or misunderstood. Be extra careful
• People sometimes forget to calculate inside the bracket first and start working outside brackets without solving things within brackets properly, which leads to calculation mistakes.

3. Confusion with Division and Multiplication

These are done in order, whichever comes first.

• People sometimes get confused about which one to do first! Remember to go in order. Whichever comes first!
• Both division and multiplication should be carried out first, following left to right rule! Then comes the addition/subtraction

4. Overlooking the Left-to-Right Rule

Multiplication/Division or addition/subtraction have a particular order (left to right)

• Sometimes, people skip the part to work in the exact left-to-right order of calculations after solving the priority parts like brackets. That leads to some wrong outcomes!
• For both division/multiplication or addition/subtraction, we need to work from left to right in calculations if those steps appear multiple times within a particular calculation sequence. The BODMAS rules are well-explained in a strict format.

5. Mishandling Negative Numbers

Negatives can cause confusion in calculations.

• People often mess up negative signs. Double check for these signs to avoid miscalculations
• Negative signs combined with other operations, including powers and roots in complex calculations need careful handling. Mismanagement of the negative numbers can alter the whole result significantly

6. Errors with Exponents/Orders

Powers/roots can trip people up.

• Sometimes, people miscalculate the powers. Always be sure the exponent (top number) part is handled properly to get the right result.
• It's easy to mistake the value or how roots operate

7. Ignoring Implicit Multiplication

Hidden multiplication signs cause confusion.

• Sometimes there aren't explicit (obvious) signs. They mean 'times.' Watch out!

Understanding and avoiding these seven common errors will improve math problem-solving and enhance one’s grip and grasp over BODMAS. Always make a conscious and mindful effort to calculate each and every step correctly, ensuring the results to match the rule. This careful practice is important.

5 Real-World Applications of BODMAS

BODMAS isn't just for schoolwork. It's a vital tool in many everyday situations.

1. Calculating Finances

BODMAS helps in financial calculations.

• Understanding discounts and surcharges (taxes) often requires careful order of operations to accurately figure the total cost. Order is key!
• Using coupons or promotions correctly in calculations, when more steps appear, is helpful.

2. Programming and Computer Science

Computers follow clear rules like BODMAS.

• Complex computer programs use BODMAS in algorithms or calculations for data processing; the order avoids errors or miscalculation, very important when multiple things appear simultaneously.



Source: amazonaws.com

• Coding follows this principle; this rule helps to ensure that the computer understands the correct operation step, even if a code line might get longer with many actions or commands included together.

3. Engineering and Construction

Engineers use precise calculations, avoiding miscalculations and errors in structures and designs.

• In engineering and construction, exact calculations like dimensioning are important to determine size and measurements, avoiding mistakes. For bridges, roads or any construction projects the correct application of calculations to create a correct output is very important to make the structures sound.

• In creating precise measurements, such as those in engineering, calculating in a certain, standard and orderly fashion helps the task be accurate. The order from which things are calculated ensures correct answers to each problem or solution set needed. The proper order of execution is needed for calculation solutions to be useful and make good engineering plans for real world usage of ideas.

  

  Source: cloudfront.net

4. Scientific Calculations

Science involves many complex calculations!

• Chemistry, physics, and other science calculations often follow rules to achieve accurate results. Calculating formulas need following steps carefully without leaving anything to doubt.
• Scientific models sometimes calculate outputs accurately. Precisely using the BODMAS will help to solve each step correctly without issues or uncertainties.

5. Everyday Problem-Solving

BODMAS even helps with simple tasks!

• Figuring tips or splitting costs properly (at restaurants or with groups) requires exact calculations based on order and sequence for getting proper results.
• Tasks with various calculations can involve the proper use of BODMAS in problem-solving using its important tools or ways, that involve working with money and various values, for many common situations at the work place or home in many settings, where accurate and complete results are important

BODMAS simplifies tricky math problems and has great value in daily tasks or special problems! Use these skills daily. Remember BODMAS!

Mastering BODMAS with Practice Exercises and Solutions

Practice makes perfect! These exercises will help you become proficient with BODMAS.

Exercise 1

This exercise focuses on basic BODMAS application.

• Solve the expressions following BODMAS rules.
• This is like starting training for any difficult sport. We need simple starts first.



Source: edulyte.com

Exercise 2

Here, you'll practice with more complex calculations and combinations of addition and subtraction with more calculations appearing.

• Expressions contain multiple steps within BODMAS rule for accurate and useful results. Getting used to tackling longer tasks will improve one’s ability to tackle difficult problems.

Exercise 3

This exercise adds powers and roots to the mix.

Source: ytimg.com

• Here, understanding powers, exponents and handling brackets or parentheses in a difficult setting will aid further practice. Practice tackling these challenging and useful mathematical parts and how the BODMAS rules aid solving these equations.



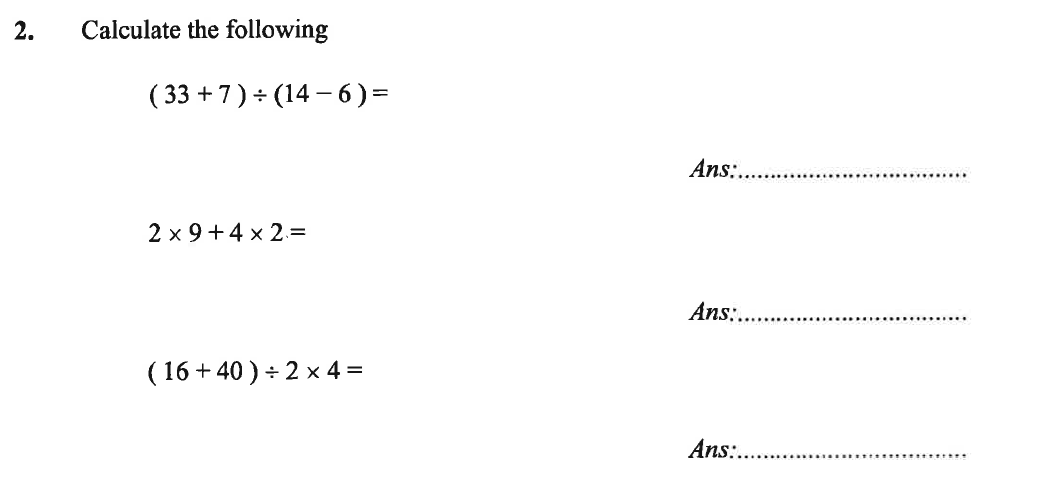
Source: co.uk

Exercise 4

Practice using nested brackets in problems to hone your BODMAS skills.

• Solving various types of expressions like addition and multiplication problems nested within various types of parenthesis or bracket solutions and equations. Practice on this level improves abilities when encountering more tricky nested types and sets, following BODMAS guidelines for complete solutions or outcomes

Exercise 5

This exercise incorporates negative numbers.

• This is another good level to understand or grasp BODMAS rules by working with more challenging or useful negative numbers. Practice to gain accuracy with numbers by working with examples containing a high degree or many levels of difficult nested types or combination parts. Make sure each step adheres to rules strictly for correct solutions.

Solving these exercises helps one to enhance calculation skills to confidently take on any challenging BODMAS problem. Using proper techniques to execute calculation solutions to math equations is necessary in handling any problems! Practicing different styles or patterns for various challenging expressions within each step of BODMAS, will improve the execution process and build your problem solving confidence significantly.

Winding Up: BODMAS Made Easy

BODMAS is a key part of math. Understanding it leads to correct answers.

Key Takeaways from BODMAS Principles

The order of operations is critical.

• Understanding BODMAS helps in consistently and correctly solving math problems, even complex ones.

• Follow the rules: solve things in brackets, exponents/orders, and finally do the division, multiplication, addition, and subtraction, in order.

• Mastering the order allows for confidence in math operations, regardless of problem types.

Additional Resources for BODMAS Practice

Practice more, practice harder

• Use online resources and websites for more BODMAS practice exercises and answers
• Practicing different levels of difficulty (starting easy then moving harder) builds your strength in math operations, by encountering various kinds of mathematical issues

Tips for BODMAS Success

Successful handling or executing of operations will result in quick and correct calculations and solutions.

• Carefully examine all operations and apply BODMAS steps by steps, precisely

• Be mindful when calculations contain both simpler addition, and division or multiplications and subtractions within calculations; the proper use of the steps and rules is important!

• Focus on one step at a time. Accuracy matters, as one wrong step leads to an overall error or mistake. The important part or section that needs attention and execution with accuracy is the order, and making the proper choices.

Understanding and using the rules consistently builds ability. The skill, built over practice helps in tackling various and multiple math problems effectively and accurately. This understanding leads to clear outcomes to difficult math expressions and formulas. Remember BODMAS!